Lógica

Lógica Proposicional

¿Qué es la Lógica?

Es la disciplina que trata sobre los métodos del razonamiento.

Proporciona reglas y técnicas para determinar si es o no válido un razonamiento.

Se emplea en matemáticas para demostrar teoremas; en informática para verificar si son o no correctos los programas.

esquema relacional que explica como se
compone la lógica proposicional .

La lógica proposicional o lógica de orden cero es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.

La lógica proposicional trata con sistemas lógicos que carecen de cuantificadores, o variables interpretables como entidades. En lógica proposicional si bien no hay signos para variables de tipo entidad, sí existen signos para variables proposicionales (es decir, que pueden ser interpretadas como proposiciones con un valor de verdad de definido), de ahí el nombre proposicional. La lógica proposicional incluye además de variables interpretables como proposiciones simples signos para conectivas lógicas, por lo que dentro de este tipo de lógica puede analizarse la inferencia lógica de proposiciones a partir de proposiciones, pero sin tener en cuenta la estructura interna de las proposiciones más simples.

Conectiva Lógica: símbolo que se utiliza para conectar dos fórmulas bien formadas (atómicas o moleculares), de modo que el valor de verdad de la fórmula compuesta depende del valor de verdad de las fórmulas componentes.

En programación se utilizan para combinar valores de verdad y obtener nuevos valores que determinen el flujo de control de un algoritmo o programa.

Las conectivas lógicas son, junto con los cuantificadores, las principales constantes lógicas de muchos sistemas lógicos, principalmente la lógica proposicional y la lógica de predicados.

En la lógica proposicional, las conectivas lógicas se tratan como funciones de verdad. Es decir, como funciones que toman conjuntos de valores de verdad y devuelven valores de verdad. Por ejemplo, la conectiva lógica "no" es una función que si toma el valor de verdad V, devuelve F, y si toma el valor de verdad F, devuelve V. Por lo tanto, si se aplica la función «no» a una letra que represente una proposición falsa, el resultado será algo verdadero. Si es falso que "está lloviendo", entonces será verdadero que "no está lloviendo".

El significado de las conectivas lógicas no es nada más que su comportamiento como funciones de verdad. Cada conectiva lógica se distingue de las otras por los valores de verdad que devuelve frente a las distintas combinaciones de valores de verdad que puede recibir. Esto quiere decir que el significado de cada conectiva lógica puede ilustrarse mediante una tabla que despliegue los valores de verdad que la función devuelve frente a todas las combinaciones posibles de valores de verdad que puede recibir.

Tabla de verdad: La tabla de verdad de una fórmula es una tabla en la que se presentan todas las posibles interpretaciones de las variables proposicionales que constituye la fórmula y el valor de verdad de la fórmula completa para cada interpretación. Por ejemplo, la tabla de verdad para la fórmula

Conectiva	Notación	Ejemplo de uso	Análogo natural	Ejemplo de uso en el lenguaje natural	Tabla de verdad 1=V; 0=F
Negación	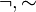$\neg,\sim \,$	$\neg p \,$	no	No está lloviendo.	$\begin{array}{c\|c} \phi & \neg \phi \\ \hline 1 & 0 \\ 0 & 1 \\ \end{array}$
Conjunción	$\and,\And, \cdot \,$	$p \and q \,$	y	Está lloviendo y la calle está mojada.	$\begin{array}{c\|c\|c} \phi & \psi & \phi \and \psi \\ \hline 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array}$
Disyunción	$\or \,$	$p \or q \,$	o	Está lloviendo o la calle está mojada.	$\begin{array}{c\|c\|c} \phi & \psi & \phi \or \psi \\ \hline 1 & 1 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \\ \end{array}$
Condicional material	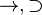$\to,\supset$	$p \to q \,$	si... entonces	Si está lloviendo, entonces la calle está mojada.	$\begin{array}{c\|c\|c} \phi & \psi & \phi \to \psi \\ \hline 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \\ \end{array}$
Bicondicional	$\leftrightarrow, \equiv \,$	$p \leftrightarrow q \,$	si y sólo si	Está lloviendo si y sólo si la calle está mojada.	$\begin{array}{c\|c\|c} \phi & \psi & \phi \leftrightarrow \psi \\ \hline 1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}$
Negación conjunta	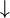$\downarrow \,$	$p \downarrow q \,$	ni... ni	Ni está lloviendo ni la calle está mojada.	$\begin{array}{c\|c\|c} \phi & \psi & \phi \downarrow \psi \\ \hline 1 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array}$
Disyunción excluyente	$\nleftrightarrow, \oplus, \not\equiv, W , \underline{\vee}$	$p \nleftrightarrow q \,$	o bien... o bien	O bien está lloviendo, o bien la calle está mojada.	$\begin{array}{c\|c\|c} \phi & \psi & \phi \nleftrightarrow \psi \\ \hline 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \\ \end{array}$

Enunciado: se llama enunciado a toda frase u oración, que se utiliza en el lenguaje común.Algunos enunciados son mandatos, interrogaciones o expresiones de emoción; otros en cambio son afirmaciones o negaciones que tienen la característica de ser verdadero o falso.

Abiertos: son enunciados que contienen "variables" y carecen de la propiedad de ser verdadero o falso, son conocidos como: "función proposicional".

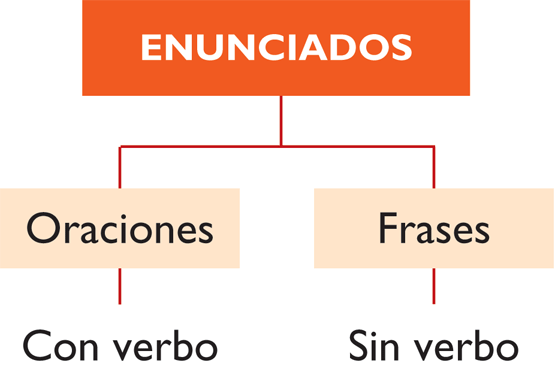
Ejemplo:

X<5 es un enunciado abierto ya que no se puede afirmar que es verdadero o falso dado

que solo cuando X toma un valor numérico se puede decir si es o no verdadero.

X=3 entonces 3<5 (V)

X=7 entonces 7<5 (F)

Proposición: enunciado cuya propiedad fundamental es ser verdadero o falso, pero no ambas a la vez y sin ambigüedad

las proposiciones lógicas se representan con letras minúsculas (a, b ,c, d, e...) llamadas "variables proposicionales".

simples ("atómicas"): son aquellas que se pueden representar con una sola variable o letra (No tiene Conectivos).

Ejemplos:

q=Pamela tiene 20 años.

p=5*6=30.

Compuestas ("moleculares"): son aquellas que están constituidas por proposiciones simples enlazadas entre si por conectivos lógicos. El valor de la verdad de una proposición compuesta depende de los valores de la verdad de las proposiciones que lo forman y de la manera como están unidas.

Ejemplos:

~p=No aprobé el curso de matemáticas.

P Λ q : Hoy es sábado y mañana es domingo.

Cortesía de Wikipedia: Lógica proposicional, conectiva lógica

Tutoriales

Teoría de conjuntos

Diagrama de Venn representando

los conjuntos hipotéticos A, B y C.

¿Que es un conjunto?: reunión, agrupación o grupo de objetos cuales quiera a los cuales se les llama elementos.

Los conjuntos son representados mediante letras mayúsculas.

Los elementos se pueden representar de cualquier forma, desde imágenes hasta letras o números, entre llaves y separados por comas.

Ejemplos:

A:{a,b,c,f,j,z}

B:{1,2,58,100}

C:{,,

}

D:{ hello, bonjour, привет... }

E:{A, B, 10*8, 3/5}

Unión entre 2 conjuntos.

Los conjuntos pueden ser representados de dos formas:

por extensión: se plasman todos los elementos.

Ejemplo: Ç:{a, b, 4, 7, chao, blog}

Por comprensión: se escribe una definición y

se le da una caracteristica comun a los elementos.

Ejemplo:D:{X/X es "hola" en otro idioma}

T:{XeZ/X^2=4} (nota: e=pertenece).

Cardinalidad: es el numero de elementos que posee un conjunto,
se denota con "n" o "#".
Ejemplo:

J={1,4,8}
n=3; #=3

El conjunto A es parte de
B que a su vez pertenece a U

Subconjuntos: un conjunto puede contener otro conjunto dentro de si por lo cual se dice que si un conjunto B esta contenido en un conjunto A, B es un subconjunto de A y se denota B⊆A.

Los subconjuntos pueden ser:

Propios: Sea B un subconjunto de A tal que B ≠ A. Entonces se dice que B es un subconjunto propio de A, dicho esto se entiende que un subconjunto de A que contenga elementos del mismo pero que a su vez no sea igual a este es un subconjunto propio.

Impropios: Se dice que todo conjunto es un subconjunto de si mismo por lo tanto si A=B entonces B es a su vez un subconjunto de A y A un subconjunto de B, por lo cual se dice que es un subconjunto impropio.

Nota: para determinar la cantidad de subconjuntos que un conjunto posee se utiliza la siguiente formula: 2^n.

Ejemplo:

G={1,5,7}
2^3=8subconjuntos
{1,5};{1,7};{5,7};{1};{5};{7};{Ø};{157}

propios

impropio

La teoría de conjuntos es una rama de las matemáticas que estudia los conceptos de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.

es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas, ...; y junto con la lógica permite estudiar los fundamentos de esta. En la actualidad se acepta que el conjunto de axiomas de la teoría de Zermelo-Fraenkel es suficiente para desarrollar toda la matemática.

Además, la propia teoría de conjuntos es objeto de estudio per se (por si mismo), no sólo como herramienta auxiliar, en particular las propiedades y relaciones de los conjuntos infinitos. En esta disciplina es habitual que se presenten casos de propiedades indemostrables o contradictorias, como la hipótesis del continuo o la existencia de un cardinal inaccesible. Por esta razón, sus razonamientos y técnicas se apoyan en gran medida en la lógica matemática.

Historia:

la teoría de conjuntos se atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas «puras» del infinitoen la segunda mitad del siglo XIX, precedido por algunas ideas de Bernhard Bolzano e influenciado por Richard Dedekind. El descubrimiento de las paradojas de la teoría cantoriana, de conjuntos, formalizada por Gottlob Frege, propició los trabajos de Bertrand Russell, Ernst Zermelo, Abraham Fraenkel y otros a principios del siglo XX.

Conjuntos mas relevantes:

Æ : el conjunto vacío, que carece de elementos.
N: el conjunto de los números naturales.
Z: el conjunto de los números enteros.
Q : el conjunto de los números racionales.
R: el conjunto de los números reales.
C: el conjunto de los números complejos.

cortesía de wikipedia: Teoría de conjuntos.

Operaciones entre conjuntos:

Unión: es la agrupación de todos los elementos de los conjuntos sin que se repita ninguno.
Intersección: se refiere a los elementos que tengan en común los conjuntos.
Diferencia: todo elemento de A que no pertenezca a B.
Diferencia simétrica: todos los elementos de A y B a excepción de sus elementos comunes.
Complemento: todos los elementos no pertenecientes al conjunto.

Lógica Proposicional

¿Qué es la Lógica?

Tutoriales

Teoría de conjuntos

Historia:

Conjuntos mas relevantes:

Operaciones entre conjuntos:

Propiedades de los conjuntos: