Teoría de conjuntos
 |
Diagrama de Venn representando
los conjuntos hipotéticos A, B y C.
|
¿Que es un conjunto?: reunión, agrupación o grupo de objetos cuales quiera a los cuales se les llama elementos.
Los conjuntos son representados mediante letras mayúsculas.
Los elementos se pueden representar de cualquier forma, desde imágenes hasta letras o números, entre llaves y separados por comas.
Ejemplos:
Los conjuntos pueden ser representados de dos formas:
- por extensión: se plasman todos los elementos.
Ejemplo: Ç:{a, b, 4, 7, chao, blog}
- Por comprensión: se escribe una definición y
Ejemplo:D:{X/X es "hola" en otro idioma}
T:{XeZ/X^2=4} (nota: e=pertenece).
Cardinalidad: es el numero de elementos que posee un conjunto,
se denota con "n" o "#".
Ejemplo:
Nota: para determinar la cantidad de subconjuntos que un conjunto posee se utiliza la siguiente formula: 2^n.
Ejemplo:
Cardinalidad: es el numero de elementos que posee un conjunto,
se denota con "n" o "#".
Ejemplo:
- J={1,4,8}
- n=3; #=3
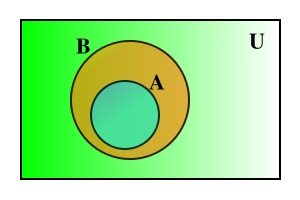 |
| El conjunto A es parte de B que a su vez pertenece a U |
Subconjuntos: un conjunto puede contener otro conjunto dentro de si por lo cual se dice que si un conjunto B esta contenido en un conjunto A, B es un subconjunto de A y se denota B⊆A.
Los subconjuntos pueden ser:
Propios: Sea B un subconjunto de A tal que B ≠ A. Entonces se dice que B es un subconjunto propio de A, dicho esto se entiende que un subconjunto de A que contenga elementos del mismo pero que a su vez no sea igual a este es un subconjunto propio.
Impropios: Se dice que todo conjunto es un subconjunto de si mismo por lo tanto si A=B entonces B es a su vez un subconjunto de A y A un subconjunto de B, por lo cual se dice que es un subconjunto impropio.
Nota: para determinar la cantidad de subconjuntos que un conjunto posee se utiliza la siguiente formula: 2^n.
Ejemplo:
- G={1,5,7}
- 2^3=8subconjuntos
- {1,5};{1,7};{5,7};{1};{5};{7};{Ø};{157}
- propios
- impropio
La teoría de conjuntos es una rama de las matemáticas que estudia los conceptos de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas. Los conjuntos y sus operaciones más elementales son una herramienta básica en la formulación de cualquier teoría matemática.
es lo suficientemente rica como para construir el resto de objetos y estructuras de interés en matemáticas: números, funciones, figuras geométricas, ...; y junto con la lógica permite estudiar los fundamentos de esta. En la actualidad se acepta que el conjunto de axiomas de la teoría de Zermelo-Fraenkel es suficiente para desarrollar toda la matemática.
Además, la propia teoría de conjuntos es objeto de estudio per se (por si mismo), no sólo como herramienta auxiliar, en particular las propiedades y relaciones de los conjuntos infinitos. En esta disciplina es habitual que se presenten casos de propiedades indemostrables o contradictorias, como la hipótesis del continuo o la existencia de un cardinal inaccesible. Por esta razón, sus razonamientos y técnicas se apoyan en gran medida en la lógica matemática.
Historia:
Historia:
la teoría de conjuntos se atribuye a Georg Cantor, que comenzó a investigar cuestiones conjuntistas «puras» del infinitoen la segunda mitad del siglo XIX, precedido por algunas ideas de Bernhard Bolzano e influenciado por Richard Dedekind. El descubrimiento de las paradojas de la teoría cantoriana, de conjuntos, formalizada por Gottlob Frege, propició los trabajos de Bertrand Russell, Ernst Zermelo, Abraham Fraenkel y otros a principios del siglo XX.
Conjuntos mas relevantes:
- Æ : el conjunto vacío, que carece de elementos.
- N: el conjunto de los números naturales.
- Z: el conjunto de los números enteros.
- Q : el conjunto de los números racionales.
- R: el conjunto de los números reales.
- C: el conjunto de los números complejos.
Operaciones entre conjuntos:
- Unión: es la agrupación de todos los elementos de los conjuntos sin que se repita ninguno.
- Intersección: se refiere a los elementos que tengan en común los conjuntos.
- Diferencia: todo elemento de A que no pertenezca a B.
- Diferencia simétrica: todos los elementos de A y B a excepción de sus elementos comunes.
- Complemento: todos los elementos no pertenecientes al conjunto.

Propiedades de los conjuntos: tutoriales recomendados:
- Identidad:
AUu=u
A∩u=A
A∩Ø=Ø
- Idempotencia:
AUA=A
A∩A=A
- Complementos:
AUA'=u
A∩A'=Ø
- Asociativa:
AU(BUC)=(AUB)UC
A∩(B∩C)=(A∩B)∩C
- Conmutativa:
AUB=BUA
A∩B=B∩A
- Distributiva:
AU(B∩C)=(AUB)∩(AUC)
A∩(BUC)=(A∩B)U(A∩C)
- Leyes de D' Morgan:
(A∩B)'=A'UB'


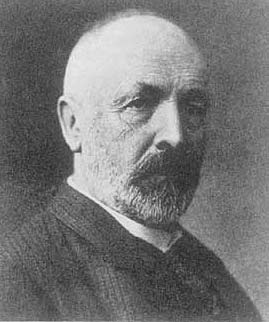
No hay comentarios:
Publicar un comentario